Kinetic energy lost in collision is 1097.95 J
Step-by-step explanation:
Given,
Mass,
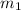 = 60 g = 0.006 kg
= 60 g = 0.006 kg
Speed,
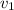 = 605 m/s
= 605 m/s
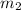 = 54 kg
= 54 kg
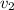 = 0
= 0
Kinetic energy lost, K×E = ?
During collision, momentum is conserved.
So,
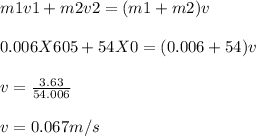
Before collision, the kinetic energy is
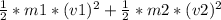
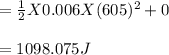
Therefore, kinetic energy before collision is 1098 J
Kinetic energy after collision:
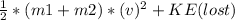
By plugging in the values, we get
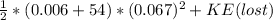
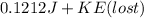
Since,
initial Kinetic energy = Final kinetic energy
1098.075 J = 0.1212 J + K×E(lost)
K×E(lost) = 1098.075 J - 0.121 J
K×E(lost) = 1097.95 J
Therefore, kinetic energy lost in collision is 1097.95 J