Question

A 60-g projectile traveling at 605 m/s strikes and becomes embedded in the 54-kg block, which is initially stationary. Compute the energy lost during the impact. Express your answer as an absolute value |ΔE| and as a percentage

Answer 1

Kinetic energy lost in collision is 1097.95 J

Step-by-step explanation:

Given,

Mass,
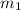`m_(1)`= 60 g = 0.006 kg

Speed,
`v_(1)` = 605 m/s

`m_(2)` = 54 kg

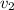`v_(2)`= 0

Kinetic energy lost, K×E = ?

During collision, momentum is conserved.

So,

`m1v1 + m2v2 = (m1 + m2)v\\\\0.006 X 605 + 54 X 0 = (0.006 + 54) v\\\\v = (3.63)/(54.006)\\ \\v = 0.067m/s`

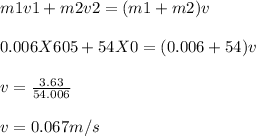
Before collision, the kinetic energy is

`(1)/(2)* m1 * (v1)^2 + (1)/(2) * m2 * (v2)^2`

`=(1)/(2) X 0.006 X (605)^2 + 0\\\\= 1098.075J`

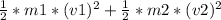
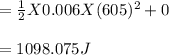
Therefore, kinetic energy before collision is 1098 J

Kinetic energy after collision:

`(1)/(2)* (m1+m2) * (v)^2 + KE(lost)`

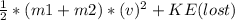
By plugging in the values, we get

`(1)/(2) * (0.006 + 54) * (0.067)^2 + KE(lost)`

`0.1212J + KE(lost)`

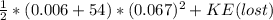
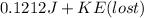
Since,

initial Kinetic energy = Final kinetic energy

1098.075 J = 0.1212 J + K×E(lost)

K×E(lost) = 1098.075 J - 0.121 J

K×E(lost) = 1097.95 J

Therefore, kinetic energy lost in collision is 1097.95 J