Answer:
A and D
Explanation:
We are given that
(3/4,2/3),(1/4,1),(1,1/2) and (1/2,1)

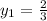
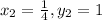
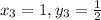
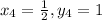
k=

Direct proportion:
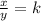
Inverse proportion:
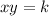

Therefore, it is not in direct proportion.
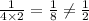

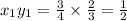
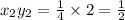

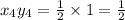
Therefore,
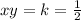
Hence, the given points form an inverse variation .

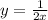
Option A and D is true.