Question

a 1-kg discus is thrown with a velocity of 19 m/s at an angle of 35 degrees from the vertical direction. calculate the vertical and horizontal velocity components.

Answer 1

15.56m/s and 10.90m/s respectively

Step-by-step explanation:

The vertical and horizontal components of a given vector, say A, are given by

`A_(Y)` = A sin θ ----------------(i)

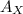`A_(X)` = A cos θ ----------------(ii)

Where;

`A_(Y)` is the vertical component of the vector A

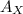`A_(X)` is the horizontal component of the vector A

A is the magnitude of the vector A

θ is the angle the vector makes with the positive x-axis (horizontal direction).

Now, from the question;

The vector is the velocity of the 1-kg discus. Lets call it vector V

The magnitude of the velocity vector V = V = 19m/s

The angle that the vector makes with the positive x-axis = θ

To calculate θ;

Notice that the velocity vector makes an angle of 35° from the vertical direction rather than the horizontal direction.

Therefore, to get the horizontal direction of the velocity vector, we subtract 35° from 90° as follows;

θ = 90° - 35° = 55°

Now, the vertical and horizontal components of the velocity vector, V, are given by

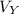`V_(Y)` = V sin θ --------------------(iii)

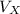`V_(X)` = V cos θ ------------------------(iv)

Substitute all the necessary values into equations(iii) and (iv) as follows;

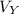`V_(Y)` = 19 sin 55° = 19m/s x 0.8192 = 15.56m/s

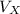`V_(X)` = 19 cos 55° = 19m/s x 0.5736 = 10.90m/s

Therefore, the vertical and horizontal velocity components are respectively 15.56m/s and 10.90m/s.

Answer 2

Vx = 10.9 m/s , Vy = 15.6 m/s

Step-by-step explanation:

Given velocity V= 19 m/s

the angle 35 ° is taken from Y-axis so the angle with x-axis will be 90°-35° = 55°

θ = 55°

to Find Vx = ? and Vy= ?

Vx = V cos θ

Vx = 19 m/s × cos 55°

Vx = 10.9 m/s

Vx = V sin θ

Vy = 19 m/s × sin 55°

Vy = 15.6 m/s