Answer:
70.31kg
Step-by-step explanation:
Step I: Consider Newton's second law of motion which states that;
∑F = m x a;
Where;
∑F = net force acting on a body
m = the mass of the body
a = acceleration due to the force on the body.
Step II: Now to the question;
Since frictional force is negligible and the only force acting on the block of ice is the applied force by the dockworker, the net force on the body (block of ice) is the constant horizontal force. i.e
∑F = 90.0N
Also;
the block starts from rest and moves a distance (s) of 13.0m in a time (t) of 4.50s. Here, we can get the acceleration in that duration of time using one
the equations of motion as follows;
s = ut +
 at² ------------------------------(ii)
at² ------------------------------(ii)
Where;
s = distance covered = 13.0m
u = initial velocity = 0 [since the block starts from rest]
t = time taken to cover the distance = 4.50s
a = acceleration of the body.
Substitute these values into equation (ii) as follows;
13.0 = 0(4.5) +
 (a)(4.50)²
(a)(4.50)²
13.0 = 0 +
 (a)(20.25)
(a)(20.25)
13.0 =
 (a)(20.25)
(a)(20.25)
13.0 = 10.125a
Solve for a;
a =
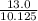
a = 1.28m/s²
Step III: Now substitute the values of a = 1.28m/s² and ∑F = 90.0N into equation (i) as follows;
90.0 = m x 1.28
m =

m = 70.31
Therefore, the mass of the block of ice is 70.31kg