Question

On average, the number of customers who had items to return for refunds or exchanges at a certain retail store's service desk is 756 per week. Find the probability that the service desk will have at least 100 customers with returns or exchanges on a randomly selected day. (Assume the store is open 7 days/week.)

Answer 1

The probability that the service desk will have at least 100 customers with returns or exchanges on a randomly selected day is P=0.78.

Explanation:

With the weekly average we can estimate the daily average for customers, assuming 7 days a week:

`M=756/7=108`

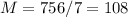
We can model this situation with a Poisson distribution, with parameter λ=108. But because the number of events is large, we use the normal aproximation:

`P(\lambda)\approx N(\lambda,\lambda)`

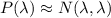
Then we can calculate the z value for x=100:

`z=(x-\mu)/(\sigma)=(100-108)/(√(108))=(-8)/(10.4) =-0.77`

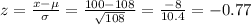
Now we calculate the probability of x>100 as:

`P(x>100)=P(z>-0.77)=0.78`

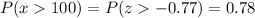
The probability that the service desk will have at least 100 customers with returns or exchanges on a randomly selected day is P=0.78.