Answer:
5732 years
Step-by-step explanation:
Radioactive decay can be determined by using the equation:

where;
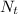 = number of decayed atoms at time (t)
= number of decayed atoms at time (t)
 = initial number of decayed atoms
= initial number of decayed atoms
 = decay constant
= decay constant
So, if we equate the natural log of the above; we have:
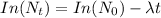
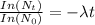
where;
 =
=
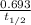
 =
=
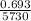
 =
=

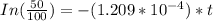
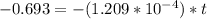

t = 5732.01 years
t = 5732 years.
Hence, the fossil is 5732 years old.