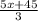Answer:
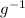 (x) =
(x) =
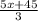
Explanation:
let y = g(x) and rearrange making x the subject
y =
 x - 9 ( add 9 to both sides )
x - 9 ( add 9 to both sides )
y + 9 =
 x
x
Multiply both sides by 5 to clear the fraction
5y + 45 = 3x ( divide both sides by 3 )
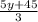 = x
= x
Change y back into terms of x, thus
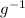 (x) =
(x) =