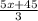Question

Find g-1(x) when g(x)=3/5x-9

Answer 1

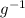`g^(-1)`(x) =
`(5x+45)/(3)`

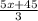
Explanation:

let y = g(x) and rearrange making x the subject

y =
`(3)/(5)` x - 9 ( add 9 to both sides )

y + 9 =
`(3)/(5)` x

Multiply both sides by 5 to clear the fraction

5y + 45 = 3x ( divide both sides by 3 )

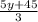`(5y+45)/(3)` = x

Change y back into terms of x, thus

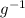`g^(-1)`(x) =
`(5x+45)/(3)`

Answer 2

The inverse is g⁻¹(x) = (5/3)*(x + 9)

How to find the inverse?

for a function f(x), the inverse f⁻¹(x) is defined as:

if f(x) = y

f⁻¹(y) = x

For this case, we can write:

g(g⁻¹(x)) = x

(3/5)*g⁻¹(x) - 9 = x

(3/5)*g⁻¹(x) = x + 9

g⁻¹(x) = (5/3)*(x + 9)