Question

Which statements are true when verifying the solution set of |6-x/3|>18 as x <-36 or x > 72?

Answer 1

Answer: 2, 3, 4, & 6.

Step-by-step explanation: edge 2021

Answer 2

Since, you have not mentioned the statements, but I am solving the expression as well as verifying which anyways may be able to make you understand the concept.

Answer:

Both
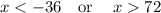`x<-36\quad \mathrm{or}\quad \:x>72` are the True solutions.

Explanation:

Considering the expression

`\left|6-(x)/(3)\right|>18`

`\mathrm{Apply\:absolute\:rule}:\quad \mathrm{If}\:|u|\:>\:a,\:a>0\:\mathrm{then}\:u\:<\:-a\:\quad \mathrm{or}\quad \:u\:>\:a`

`6-(x)/(3)<-18\quad \mathrm{or}\quad \:6-(x)/(3)>18`

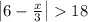
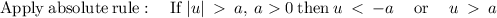
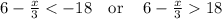
solving

`6-(x)/(3)<-18`

`6-(x)/(3)-6<-18-6`

`-(x)/(3)<-24`

`3\left(-(x)/(3)\right)<3\left(-24\right)`

`\mathrm{Multiply\:both\:sides\:by\:-1\:\left(reverse\:the\:inequality\right)}`

`\left(-x\right)\left(-1\right)>\left(-72\right)\left(-1\right)`

`x>72`

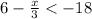
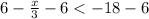
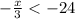
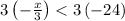
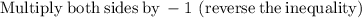
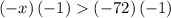
also solving

`6-(x)/(3)>18`

`6-(x)/(3)-6>18-6`

`-(x)/(3)>12`

`-x>36`

`\mathrm{Multiply\:both\:sides\:by\:-1\:\left(reverse\:the\:inequality\right)}`

`\left(-x\right)\left(-1\right)<36\left(-1\right)`

`x<-36`

`\mathrm{Combine\:the\:intervals}`

`x<-36\quad \mathrm{or}\quad \:x>72`

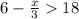
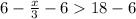
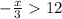
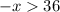
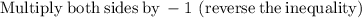
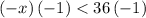
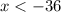
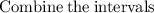
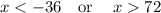
Verifying the solution:

Putting the value x < -36 in
`\left|6-(x)/(3)\right|>18`

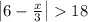
let suppose x = -37 which is < -36

`\left|6-(x)/(3)\right|>18`

`\left|6-(\left(-37\right))/(3)\right|>18`

`\mathrm{Apply\:rule}\:-\left(-a\right)=a`

`=\left|6+(37)/(3)\right|`

`=\left|(55)/(3)\right|`

`\mathrm{Apply\:absolute\:rule}:\quad \left|a\right|=a,\:a\ge 0`

`(55)/(3)>18`

`\mathrm{Therefore,\:the\:solution\:is}`

`\mathrm{True}`

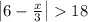
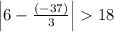
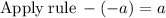
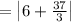
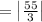
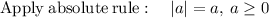
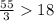
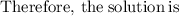
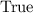
also putting the value x > 72

let suppose x = 73 which is > 72

`|6-(\left(73\right))/(3)|>\:18`

`=\left|-(55)/(3)\right|`

`\mathrm{Apply\:absolute\:rule}:\quad \left|-a\right|=a`

`=(55)/(3)`

`(55)/(3)>18`

`\mathrm{Therefore,\:the\:solution\:is}`

`\mathrm{True}`

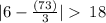
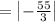
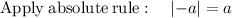
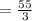
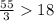
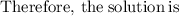
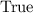
So, both
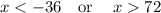`x<-36\quad \mathrm{or}\quad \:x>72` are the True solutions.