Question

The slope of a line is ¾.  A different line passes through the points (6, 3) & (-1, 5).  Are the lines parallel?  Why or why not?

Group of answer choices

A They are parallel because they both have a slope of ¾.

B They are not parallel because their slopes are not equal.

C They are parallel because they share a common point.

D They are not parallel because they are the exact same line.



​

Answer 1

They are not parallel because their slopes are not equal.

Solution:

Given that,

`\text{ slope of line } =(3)/(4)`

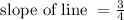
A different line passes through the points (6, 3) & (-1, 5)

Find the slope of this line

`m = (y_2-y_1)/(x_2-x_1)`

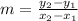
From given,

`(x_1, y_1) = (6, 3)\\\\(x_2, y_2) = (-1, 5)`

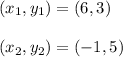
Substituting we get,

`m = (5-3)/(-1-6)\\\\m = (2)/(-7)`

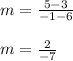
For two lines are parallel, then their slopes must be equal

But here,

`(3)/(4) \\eq (-2)/(7)`

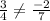
Therefore, They are not parallel because their slopes are not equal