Answer:
(a) Speed of baseball is 31.03 m/s
(b) Bullet has greater kinetic energy than baseball
Step-by-step explanation:
Given :
Mass of baseball, M = 0.145 kg
Mass of bullet, m = 3 g = 3 x 10⁻³ kg
Speed of bullet, v = 1.50 x 10³ m/s
Let u m/s be the speed of the baseball.
(a)
According to the problem, momentum of bullet and momentum of baseball is same. So,
M x u = m x v
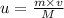
Substitute the values of m, M and v in the above equation.
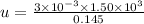
u = 31.03 m/s
(b) Kinetic energy of baseball is given by the relation :
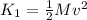
Substitute the values of M and v in the above equation.
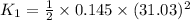
K₁ = 69.80 J
Kinetic energy of bullet is given by the relation :

Substitute the values of M and v in the above equation.
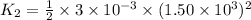
K₂ = 3375 J
Since, K₂ is greater than K₁, hence bullet has greater kinetic energy than baseball.