Answer:

And replacing we got:
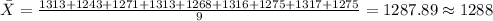
In order to find the sample deviation we can use this formula:
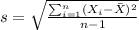
s= \sqrt{\frac{(1313-1287.89)^2 +(1243-1287.89)^2 +(1271-1287.89)^2 +(1313-1287.89)^2 +(1268-1287.89)^2 + (1316-1287.89)^2 +(1275-1287.89)^2 +(1317-1287.89)^2 +(1275-1287.89)^2}{9-1}}= 27.218 \approx 27
Explanation:
For this case we have the following data given:
1313 1243 1271 1313 1268 1316 1275 1317 1275
In order to calculate the sample mean we can use the following formula:

And replacing we got:
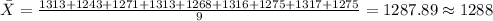 In order to find the sample deviation we can use this formula:
In order to find the sample deviation we can use this formula:
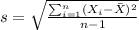
And replacing we have:
s= \sqrt{\frac{(1313-1287.89)^2 +(1243-1287.89)^2 +(1271-1287.89)^2 +(1313-1287.89)^2 +(1268-1287.89)^2 + (1316-1287.89)^2 +(1275-1287.89)^2 +(1317-1287.89)^2 +(1275-1287.89)^2}{9-1}}= 27.218 \approx 27