Question

The method of tree ring dating gave the following years A.D. for an archaeological excavation site. Assume that the population of x values has an approximately normal distribution. 1313 1243 1271 1313 1268 1316 1275 1317 1275 (a) Use a calculator with mean and standard deviation keys to find the sample mean year x and sample standard deviation s. (Round your answers to the nearest whole number.) x

Answer 1

`\bar X = (\sum_(i=1)^n X_i)/(n)`

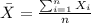
And replacing we got:

`\bar X = (1313+1243+1271+1313+1268+1316+1275+1317+1275)/(9)=1287.89 \approx 1288`

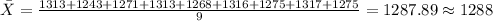
In order to find the sample deviation we can use this formula:

`s= \sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)}`

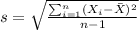
s= \sqrt{\frac{(1313-1287.89)^2 +(1243-1287.89)^2 +(1271-1287.89)^2 +(1313-1287.89)^2 +(1268-1287.89)^2 + (1316-1287.89)^2 +(1275-1287.89)^2 +(1317-1287.89)^2 +(1275-1287.89)^2}{9-1}}= 27.218 \approx 27

Explanation:

For this case we have the following data given:

1313 1243 1271 1313 1268 1316 1275 1317 1275

In order to calculate the sample mean we can use the following formula:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

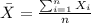
And replacing we got:

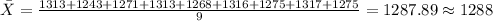`\bar X = (1313+1243+1271+1313+1268+1316+1275+1317+1275)/(9)=1287.89 \approx 1288`In order to find the sample deviation we can use this formula:

`s= \sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)}`

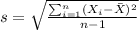
And replacing we have:

s= \sqrt{\frac{(1313-1287.89)^2 +(1243-1287.89)^2 +(1271-1287.89)^2 +(1313-1287.89)^2 +(1268-1287.89)^2 + (1316-1287.89)^2 +(1275-1287.89)^2 +(1317-1287.89)^2 +(1275-1287.89)^2}{9-1}}= 27.218 \approx 27