Answer:
The rate of study is 5 items per hour.
Explanation:
Number of items a person can learn after t hours of instruction, w(t) is given by:
![w(t)=15\sqrt[3]{t^(2)}](https://img.qammunity.org/2021/formulas/mathematics/college/dk7vl6o7cph3ijkqk7qjfsrogrcagymfjz.png)
We want to determine the rate of learning at any time t. The rate is the derivative of w(t) with respect to time.
![(dw(t))/(dt) =(d)/(dt) 15\sqrt[3]{t^(2)}](https://img.qammunity.org/2021/formulas/mathematics/college/l5n7v1abjytddm8n27d8kb7ed0tvstcbp6.png)
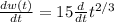
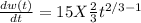

Therefore, the rate of learning at any time t
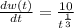
At the end of 8 hours, t=8
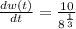
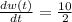 =5
=5
The rate of study is 5 items per hour.