Question

According to one theory of learning, the number of items, w(t), that a person can learn after t hours of instruction is given by: w(t) = 15 3 t2, 0 ≤ t ≤ 64 Find the rate of learning at the end of eight hours of instruction.

Answer 1

The rate of study is 5 items per hour.

Explanation:

Number of items a person can learn after t hours of instruction, w(t) is given by:

`w(t)=15\sqrt[3]{t^(2)}`

We want to determine the rate of learning at any time t. The rate is the derivative of w(t) with respect to time.

`(dw(t))/(dt) =(d)/(dt) 15\sqrt[3]{t^(2)}`

`(dw(t))/(dt) =15(d)/(dt) {t^(2/3)}`

`(dw(t))/(dt) =15X(2)/(3) {t^(2/3-1)}`

`(dw(t))/(dt) =10 {t^{-(1)/(3) }}=(10)/(t^(1)/(3))`

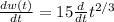
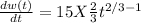
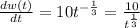
Therefore, the rate of learning at any time t

`(dw(t))/(dt) =(10)/(t^(1)/(3))`

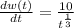
At the end of 8 hours, t=8

`(dw(t))/(dt) =(10)/(8^(1)/(3))`

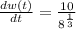
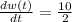`(dw(t))/(dt) =(10)/(2)`=5

The rate of study is 5 items per hour.