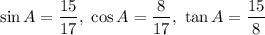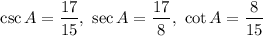The value of each trigonometric ratio is
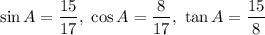
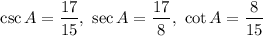
Solution:
The given triangle is right triangle.
AC (hypotenuse) = 34, AB (adjacent) = 16, BC (opposite) = 30
To find the trigonometric ratios:
Using trigonometric formulas for right triangle,
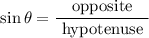
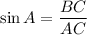
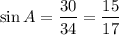
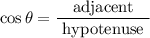
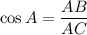
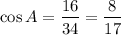
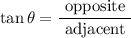
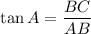
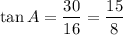
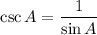
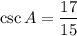
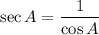
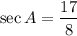
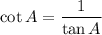
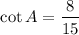
Hence the value of each trigonometric ratio is