Question

Vangaurd Health System bonds have an annual coupon rate of 8 percent and a par value of $1,000 and will mature in 20 years. If you require a 7 percent return, what price would you be willing to pay for a Vangaurd bond

Answer 1

Price willing to pay=$1105.94

Step-by-step explanation:

Annual Coupon Payment=$1,000*0.08

Annual Coupon Payment=$80

Calculating Present Value (PV) of Par Value:

`PV=(FV)/((1+i)^(20))`

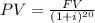
Where:

i is the rate of return.

FV is par value

`PV=(\$1000)/((1+0.07)^(20))`

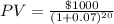
PV= $258.419.

Calculating PV of annual Coupon Payment:

`PV=A(1-(1+i)^(-20))/(i)`

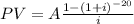
i is the coupon rate

A is the annual Payment

`PV=\$80(1-(1+0.07)^(-20))/(0.07)`

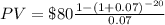
PV=$847.521

Price willing to pay= Present Value (PV) of Par Value+ PV of annual Coupon Payment

Price willing to pay=$258.419+$847.521

Price willing to pay=$1105.94