Answer:
(a). The speed of the ball after collision is 2.01 m/s.
(b). The speed of the block after collision 1.11 m/s.
Step-by-step explanation:
Suppose, A steel ball of mass 0.500 kg is fastened to a cord that is 50.0 cm long and fixed at the far end. The ball is then released when the cord is horizontal.
Given that,
Mass of steel block = 2.30 kg
Mass of ball = 0.500 kg
Length of cord = 50.0 cm
We need to calculate the initial speed of the ball
Using conservation of energy
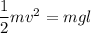
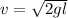
Put the value into the formula
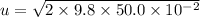
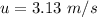
The initial speed of the ball
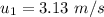
The initial speed of the block
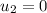
(a). We need to calculate the speed of the ball after collision
Using formula of collision
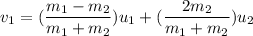
Put the value into the formula
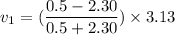
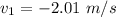
Negative sign shows the opposite direction of initial direction.
(b). We need to calculate the speed of the block after collision
Using formula of collision
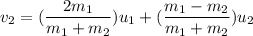
Put the value into the formula
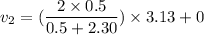
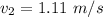
Hence, (a). The speed of the ball after collision is 2.01 m/s.
(b). The speed of the block after collision 1.11 m/s.