Question

Given that the acceleration of gravity at the surface of Mars is0.38 of what it is one Earth, and that Mars' radius is 3400 km,determine the mass of Mars.

Answer 1

`1.156* 10^(24)\ kg`

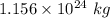
Step-by-step explanation:

Given:

Gravity of Mars = 0.38 times the gravity at Earth

Gravity of Earth is,
`g_(Earth)=9.8\ m/s^2`

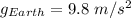
Radius of Mars (R) = 3400 km

Mass of mars (M) = ?

We know that, the acceleration due to gravity of a planet of mass 'M' and radius 'R' is given as:

`g=(GM)/(R^2)`

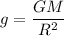
Now, as per question:

`g_(Mars)=0.68g_(Earth)`

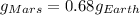
Plug in 9.8 for
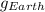`g_(Earth)` and solve for
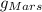`g_(Mars)`. This gives,

`g_(Mars)=0.68* 9.8=6.67\ m/s^2`

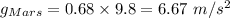
Now, plug in this value in the above equation and solve for 'M'. This gives,

`6.67=(6.67* 10^(-11)M)/((3400* 10^3)^2)\\\\1.156* 10^(13)=10^(-11)M\\\\M=(1.156* 10^(13))/(10^(-11))\\\\M=1.156* 10^(24)\ kg`

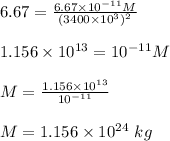
Therefore, the mass of Mars is
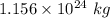`1.156* 10^(24)\ kg`.