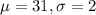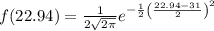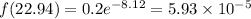Answer:
a) 22.94 psi
b)
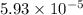
Explanation:
a)The pressure at which will trigger a warning is
31 - 31*0.26 = 22.94 psi
b) The probability that that the TPMS will trigger warning at 22.94 psi, given that tire pressure has a normal distribution with average of 31 psi and standard deviation of 2 psi
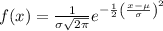
where x = 22.94,