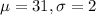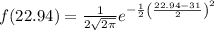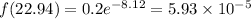Question

Tire pressure monitoring systems (TPMS) warn the driver when the tire pressure of the vehicle is 26% below the target pressure. Suppose the target tire pressure of a certain car is 31 psi (pounds per square inch.)(a) At what psi will the TPMS trigger a warning for this car?(b) Suppose tire pressure is a normally distributed random variable with a standard deviation equal to 2 psi. If the car's average tire pressure is on target, what is the probability that the TPMS will trigger a warning?

Answer 1

a) 22.94 psi

b)
`5.93*10^(-5)`

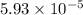
Explanation:

a)The pressure at which will trigger a warning is

31 - 31*0.26 = 22.94 psi

b) The probability that that the TPMS will trigger warning at 22.94 psi, given that tire pressure has a normal distribution with average of 31 psi and standard deviation of 2 psi

`f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^(2)}`

where x = 22.94,
`\mu = 31, \sigma = 2`

`f(22.94)={\frac {1}{2 {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {22.94-31}{2 }}\right)^(2)}`

`f(22.94)=0.2e^(-8.12) = 5.93*10^(-5)`