Answer:
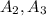 are not independent events.
are not independent events.
Explanation:
We are given the following in the question:
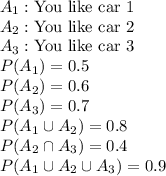
Independent events:
- Two events A and B is said to be independent if
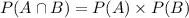
Since,
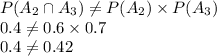
Thus, they are not independent events.
Now, we evaluate

Thus, they are not independent event.