Question

A source emits sound uniformly in all directions. A radial line is drawn from this source. On this line, determine the positions of two points, 0.94 m apart, such that the intensity level at one point is 2.12 dB greater than the intensity level at the other. (Enter your answers from smallest to largest.)

Answer 1

Positions of two points are : 3.4 m and 4.3 m.

Step-by-step explanation:

Let two distance be r and r+0.94.

Now intensity at r,
`I_(1\\)` =
`(P)/(4 \pi r^(2) )`

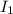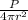
intensity at (r+0.94),
`I_(2)` =
`(P)/(4 \pi (r+0.94)^(2) )`

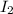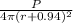
Now for decibel,

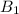`B_(1)` = 10 log (
`(I_(1) )/(I_(0) )`)

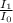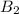`B_(2)` = 10 log (
`(I_(2) )/(I_(0) )`)

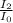As given on question:

`B_(1)` -
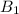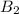`B_(2)` = 2.12 dB

⇒ 2.12 dB = 10 log (
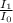`(I_(1) )/(I_(0) )`) - 10 log (
`(I_(2) )/(I_(0) )`)

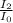⇒0.212 = log (
`(I_(1) )/(I_(2) )`)

⇒
`(I_(1) )/(I_(2) )` =
`10^(0.212)`

⇒
`((r+0.94)^(2) )/(r^(2) )` =
`10^(0.212)`

⇒
`(r+0.94)/(r)` =
`10^(0.106)`

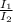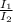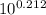
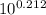
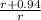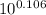
⇒ r= 3.4 m, r+0.94= 4.3 m

Hence the position of two points is 3.4 m and 4.3 m.