Question

StartLayout Enlarged left-brace 1st row x² + y² = 25 2nd row 2x + y = 25 EndLayout 0, –5) and (–5, 5) (0, –5) and (5, –15) (0, –5) and (–4, 3) (0, –5) and (4, –13)

Answer 1

The line does not intersect the curve

Explanation:

Assuming that we are looking for the points of intersection of

`{x}^(2) + {y}^(2) = 25`

and

`2x + y = 25`

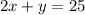
We make y the subject in the second equation to get:

`y = 25 - 2x`

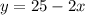
When we substitute into the first equation:

`{x}^(2) + {(25 -2 x)}^(2) = 25`

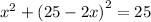
Let us expand to get:

`{x}^(2) + 625 - 100x + 4 {x}^(2) = 25`

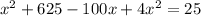
We obtain the standard form

`5 {x}^(2) - 100x + 600 = 0`

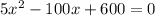
Divide through by 5

`{x}^(2) - 20x + 120 = 0`

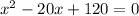
The discriminant is

`{( - 20)}^(2) - 4 * 1 * 120 = - 80`

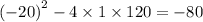
Hence the quadratic equation has no real roots.

This means the line and point has no point of intersection.

Answer 2

C. (0,-5) (-4,3)

Explanation: