Answer:
The answer is y = ±
![\sqrt[4]{(x)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/sfxin5ohpt4oo3rua6gzkn7oe6ekl66o6u.png) ,
,
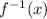 is a function ⇒ 1st answer
is a function ⇒ 1st answer
Explanation:
Let us revise the steps of find the inverse of a function
- Replace f(x) with y
- Replace every x by y and replace y by x
- Solve the equation in Step 2 for y
- Replace y by
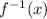
∵

- Replace f(x) by y
∴
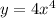
- Replace y by x and x by y
∴
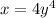
- Divide each side by 4
∴
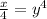
- Take
![\sqrt[4]{}](https://img.qammunity.org/2021/formulas/engineering/college/87zkin7efptxv6sfmcxawpo4w24wea2n6c.png) for both sides
for both sides
∴ ±
![\sqrt[4]{(x)/(4)}=y](https://img.qammunity.org/2021/formulas/mathematics/high-school/fz3omq7wvz464e52idsm85ykd63s7af9ug.png)
- Switch the two sides
∴ y = ±
![\sqrt[4]{(x)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/sfxin5ohpt4oo3rua6gzkn7oe6ekl66o6u.png)
∵ There is no fourth root for negative number
∴ x ≥ 0
When you test the graph of
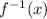 by a vertical line, it will cut it just at one in every position, so it is a function. Look to the attached graph for more understand
by a vertical line, it will cut it just at one in every position, so it is a function. Look to the attached graph for more understand
∴
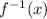 is a function
is a function
The answer is y = ±
![\sqrt[4]{(x)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/sfxin5ohpt4oo3rua6gzkn7oe6ekl66o6u.png) ,
,
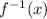 is a function
is a function