Question

Compute the marginal - revenue product fraction numerator d r over denominator d n end fraction (in dollars per employee)for a manufacturer with 5 workers if the demand function is p equals D left parenthesis x right parenthesis space equals space fraction numerator 200 over denominator square root of x end fraction and if x = 45(n). (Give answer rounded off to the nearest dollar.)

Answer 1

Demand function
`\mathrm{P}=\mathrm{D}(\mathrm{x})=210 / \mathrm{sqrt}(\mathrm{x})`

Marginal revenue = the number of items sold, x, times the price, p

Now, we are given the demand function as
`\mathrm{p}=210 / \mathrm{sqrt}(\mathrm{x})`

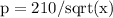
where x is the demand for units at a given price, p

=> Marginal revenue =
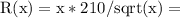`\mathrm{R}(\mathrm{x})=\mathrm{x} * 210 / \mathrm{sqrt}(\mathrm{x})=` 210 multilply with sqrt(x) , --------------->(1)

Now, we need to find the marginal revenue hen x = 45 units , so we'll plug x = 45 in equation (1)

=> R(x) = 210 multiply with sqrt(45) = 1408.7228

Hence the marginal revenue is = $ 1409