Question:
Triangle DEF is congruent to right triangle GHI with a right angle at vertex H. If the slope of DE is –2, what must be true?
A. The slope of HI is 1/2.
B. The slope of EF is 1/2.
C. The slope of GH is –2.
C. The slope of DF is –2.
Answer:
The slope of HI is 1/2
The slope of EF is 1/2
Solution:
Given that,
Triangle DEF is congruent to right triangle GHI
Which means,
These pairs of angles are congruent
{D, G}, {E, H}, and {F, I}
In triangle DEF, E is a right angle
This means that the line segments
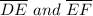 are perpendicular.
are perpendicular.
We know that,
Product of slope of a line and slope of line perpendicular to that line is equal to -1
Given that,
Slope of DE = -2
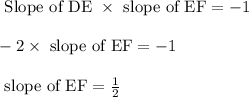
Since the sides EF and HI are congruent,
Slopes of parallel lines are equal
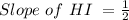
Thus, Slope of HI is 1/2