Question

Triangle DEF is congruent to right triangle GHI with a right angle at vertex H. If the slope of DE is –2, what must be true?

The slope of HI is.
The slope of EF is.
The slope of GH is –2.
The slope of DF is –2.

Answer 1

It is A

Explanation:

It is right because i got it right on edge.

Answer 2

Question:

Triangle DEF is congruent to right triangle GHI with a right angle at vertex H. If the slope of DE is –2, what must be true?

A. The slope of HI is 1/2.

B. The slope of EF is 1/2.

C. The slope of GH is –2.

C. The slope of DF is –2.

Answer:

The slope of HI is 1/2

The slope of EF is 1/2

Solution:

Given that,

Triangle DEF is congruent to right triangle GHI

Which means,

These pairs of angles are congruent

{D, G}, {E, H}, and {F, I}

In triangle DEF, E is a right angle

This means that the line segments
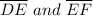`\overline{DE}\ and\ \overline{EF}` are perpendicular.

We know that,

Product of slope of a line and slope of line perpendicular to that line is equal to -1

Given that,

Slope of DE = -2

`\text{ Slope of DE } * \text{ slope of EF} = -1\\\\-2 * \text{ slope of EF} = -1\\\\\text{ slope of EF} = (1)/(2)`

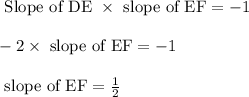
Since the sides EF and HI are congruent,

Slopes of parallel lines are equal

`Slope\ of\ HI\ = (1)/(2)`

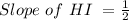
Thus, Slope of HI is 1/2