Question

What are the zeros of the quadratic function f(x) = 2x2 + 16x – 9?

x = –4 – StartRoot StartFraction 7 Over 2 EndFraction EndRoot and x = –4 + StartRoot StartFraction 7 Over 2 EndFraction EndRoot
x = –4 – StartRoot StartFraction 25 Over 2 EndFraction EndRoot and x = –4 + StartRoot StartFraction 25 Over 2 EndFraction EndRoot
x = –4 – StartRoot StartFraction 21 Over 2 EndFraction EndRoot and x = –4 + StartRoot StartFraction 21 Over 2 EndFraction EndRoot
x = –4 – StartRoot StartFraction 41 Over 2 EndFraction EndRoot and x = –4 + StartRoot StartFraction 41 Over 2 EndFraction EndRoot

Answer 1

the answer is d

Explanation:

x = –4 – StartRoot StartFraction 41 Over 2 EndFraction EndRoot and x = –4 + StartRoot StartFraction 41 Over 2 EndFraction EndRoot

Answer 2

x = - 4 ±
`\sqrt{(41)/(2) }`

Explanation:

Given

f(x) = 2x² + 16x - 9

To find the zeros, let f(x) = 0, that is

2x² + 16x - 9 = 0

Using the method of completing the square

The coefficient of the x² term must be 1

Factor out 2 from 2x² + 16x

2(x² + 8x) - 9 = 0

add/ subtract ( half the coefficient of the x- term )² to x² + 8x

2(x² + 2(4)x + 16 - 16) - 9 = 0

2(x + 4)² - 32 - 9 = 0

2(x + 4)² - 41 = 0 ( add 41 to both sides )

2(x + 4)² = 41 ( divide both sides by 2 )

(x + 4)² =
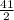`(41)/(2)` ( take the square root of both sides )

x + 4 = ±
`\sqrt{(41)/(2) }` ( subtract 4 from both sides )

x = - 4 ±
`\sqrt{(41)/(2) }`

Thus

x = - 4 +
`\sqrt{(41)/(2) }` or x = - 4 +
`\sqrt{(41)/(2) }`