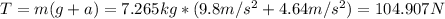Question

A bowling ball weighing 71.2 N (16.0 lb) is attached to the ceiling by a 3.80-m rope. The ball is pulled to one side and released; it then swings back and forth as a pendulum. As the rope swings through the vertical, the speed of the bowling ball is 4.20 m/s. At this instant, what are (a) the acceleration of the bowling ball, in magnitude and direction, and (b) the tension in the rope?

Answer 1

a) For this case we want to find the acceleration of the bowling ball, and we now that the only acceleration for this case would be the centrifugal acceleration becuase since the pendulum is in phase with the equilibrium point the tangential acceleration is 0, and if we find the centrifugal acceleration we got:

`a= (v^2)/(R)= ((4.2 m/s)^2)/(3.8 m)=4.64 m/s^2`

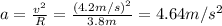
b) For this case the tendsion is an opposite force against the weight and the centrifugal force acting in the ball so then we can find the tension like this:

`T= mg +ma`

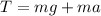
In order to find the mass we know that
`W=mg` and solving for m we got:

`m =(W)/(g)=(71.2 N)/(9.8 m/s^2)=7.265 kg`

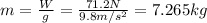
And replacing into the tension we got:

`T= m(g+a) =7.265 kg *(9.8 m/s^2 +4.64 m/s^2)=104.907 N`

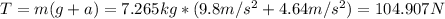
Step-by-step explanation:

For this case we have the following data given:

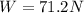`W= 71.2 N` represent the weigth for the object

`R=3.8 m` the length of the rope or the radius

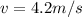`v= 4.2 m/s` represent the velocity of the bowling ball

Part a

For this case we want to find the acceleration of the bowling ball, and we now that the only acceleration for this case would be the centrifugal acceleration becuase since the pendulum is in phase with the equilibrium point the tangential acceleration is 0, and if we find the centrifugal acceleration we got:

`a= (v^2)/(R)= ((4.2 m/s)^2)/(3.8 m)=4.64 m/s^2`

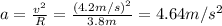
Part b

For this case the tendsion is an opposite force against the weight and the centrifugal force acting in the ball so then we can find the tension like this:

`T= mg +ma`

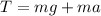
In order to find the mass we know that
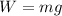`W=mg` and solving for m we got:

`m =(W)/(g)=(71.2 N)/(9.8 m/s^2)=7.265 kg`

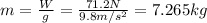
And replacing into the tension we got:

`T= m(g+a) =7.265 kg *(9.8 m/s^2 +4.64 m/s^2)=104.907 N`