Answer:
Energy of scattered photon is 232.27 keV.
Kinetic energy of recoil electron is 497.73 keV.
The recoil angle of electron is 13.40°
Step-by-step explanation:
The energy of scattered photon is given by the relation :
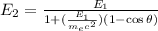 .....(1)
.....(1)
Here E₁ is the energy of incident photon, E₂ is the energy of scattered photon,
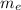 is mass of electron and θ is scattered angle.
is mass of electron and θ is scattered angle.
Substitute 730 keV for E₁, 511 keV for
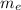 and 120° for θ in equation (1).
and 120° for θ in equation (1).
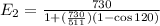
E₂ = 232.27 keV
Kinetic energy of recoil electron is given by the relation :
K.E. = E₁ - E₂ = (730 - 232.27 ) keV = 497.73 keV
The recoil angle of electron is given by :
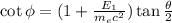
Substitute the suitable values in above equation.

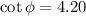
 = 13.40°
= 13.40°