Question

A 730-keV gamma ray Compton-scatters from an electron. Find the energy of the photon scattered at 120°, the kinetic energy of the scattered electron, and the recoil angle of the electron.

Answer 1

Energy of scattered photon is 232.27 keV.

Kinetic energy of recoil electron is 497.73 keV.

The recoil angle of electron is 13.40°

Step-by-step explanation:

The energy of scattered photon is given by the relation :

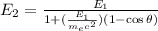`E_(2)=(E_(1) )/(1+((E_(1) )/(m_(e)c^(2) ))(1-\cos\theta) )` .....(1)

Here E₁ is the energy of incident photon, E₂ is the energy of scattered photon,
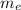`m_(e)` is mass of electron and θ is scattered angle.

Substitute 730 keV for E₁, 511 keV for
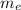`m_(e)` and 120° for θ in equation (1).

`E_(2)=(730 )/(1+((730 )/(511 ))(1-\cos120) )`

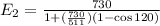
E₂ = 232.27 keV

Kinetic energy of recoil electron is given by the relation :

K.E. = E₁ - E₂ = (730 - 232.27 ) keV = 497.73 keV

The recoil angle of electron is given by :

`\cot\phi=(1+(E_(1) )/(m_(e)c^(2) ))\tan(\theta)/(2)`

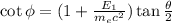
Substitute the suitable values in above equation.

`\cot\phi=(1+(730 )/(511 ))\tan(120)/(2)`

`\cot\phi=4.20`

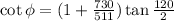
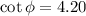
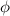`\phi` = 13.40°