Question

A motor must lift a 1300-kg elevator cab. The cab's maximum occupant capacity is 400 kg, and its constant "cruising" speed is 1.6 m/s . The design criterion is that the cab must achieve this speed within 2.0 s at constant acceleration, beginning from rest.A. When the cab is carrying its maximum capacity, at what average rate must the motor deliver energy to get the cab up to cruising speed?

Express your answer with the appropriate units.

B.At what constant rate must the motor supply energy as the fully loaded cab rises after attaining cruising speed?
Express your answer to two significant figures and include the appropriate units.

Answer 1

A. Rate of energy = 14429.6 J/s

B. Rate of energy = 27000 J/s (rounded to two significant figures)

Step-by-step explanation:

A. Total weight of cab and occupants = 1300 + 400 = 1700 kg

Change in speed = 1.6 m/s

Time taken for change in speed = 2 seconds

We can find the change in kinetic energy of the lift and occupants:

Kinetic energy at rest = 0.5 * mass * Velocity ^2

Kinetic energy at rest = 0.5 * 1700 * 0^2

Kinetic energy at rest = 0 J

Kinetic energy at cruising speed = 0.5 * mass * velocity^2

Kinetic energy at cruising speed = 0.5 * 1700 * 1.6^2

Kinetic energy at cruising speed = 2176 J

Change in energy (kinetic) = work =2176 J

We also need to account for the change in potential energy:

`v^2 - u^2 = 2*a*s`

`1.6^2 - 0^2 = 2 * 0.8 * s`

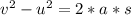
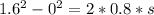
s = distance = 1.6 m

Since distance is the increase in height, we have the potential energy equal to:

Potential energy = mass * gravity * height

Potential energy = 1700 * 9.81 * 1.6

Potential energy = 26683.2 J

Total work done = 26683.2 + 2176 = 28859.2 J

Since the time taken for this work is 2 seconds, the rate at which energy is required is as follows:

Rate of energy = 28859.2 / 2 = 14429.6 J/s

B. After attaining constant speed, the only energy needed is to account for the change in gravitational potential energy. We can calculate this as follows:

Change in height = Speed * time = 1.6 * 1 = 1.6 meters

Gain in potential energy (per second) = 1700 * 9.81 * 1.6

Gain in potential energy (per second) = 26683.2 J

Rate = 26683.2 J/s

This equals the energy needed per second after attaining cruising speed.