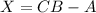Question

If​ A, B, and C are n times nn×n invertible​ matrices, does the equation Upper C Superscript negative 1 Baseline (Upper A plus Upper X )Upper B Superscript negative 1 Baseline equals Upper I Subscript nC−1(A+X)B−1=In have a solution​ X? If​ so, find it.Select the correct choice below and, if necessary, fill in the answer box within your choice. A. The solution is X=___B. There is no solution

Answer 1

Looks like the matrix equation is supposed to be

`C^(-1)(A+X)B^(-1)=I_n`

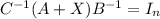
where
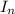`I_n` presumably denotes the
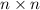`n* n` identity matrix.

Since
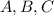`A,B,C` are all invertible, we have by multiplying on the left by
`C`,

`C(C^(-1)(A+X)B^(-1))=CI_n`

`(CC^(-1))((A+X)B^(-1))=C`

`(A+X)B^(-1)=C`

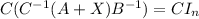
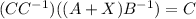
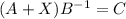
then multiplying on the right by
`B`,

`((A+X)B^(-1))B=CB`

`(A+X)(B^(-1)B)=CB`

`A+X=CB`

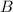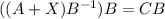
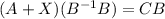
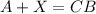
and finally subtracting
`A` from both sides to end up with

`X=CB-A`