Question

The length of time needed to complete a certain test is normally distributed with mean 57 minutes and standard deviation 8 minutes. a. What is the relative frequency of people who take between 49 and 65 minutes to complete the test? Sketch the distribution and shade in the area in question. b. Find the interval that contains the middle 95% of completion times for all people taking the test.

Answer 1

(a) The relative frequency of people who take between 49 and 65 minutes to complete the test is 0.6826.

(b) The middle 95% of completion times for all people taking the test is in the interval (41, 73).

Explanation:

Let X = length of time required complete a certain test.

It is provided that X follows a Normal distribution with mean, μ = 57 minutes and standard deviation, σ = 8 minutes.

(a)

Compute the probability of people who take between 49 and 65 minutes to complete the test as follows:

`P(49<X<65)=P((49-57)/(8)<(X-\mu)/(\sigma) <(65-57)/(8))\\=P(-1<Z<1)\\=P(Z<1)-P(Z<-1)\\=P(Z<1)-[1-P(Z<1)]\\=2P(Z<1)-1\\=(2*0.8413)-1\\=0.6826`

*Use the z-table for the probability.

Thus, the relative frequency of people who take between 49 and 65 minutes to complete the test is 0.6826.

The graph is provided below.

(b)

According to the Empirical rule, for a normal distribution:

• 68% of the observation fall within 1 standard deviation of mean.

• 95% of the observation fall within 2 standard deviation of mean.

• 99.7% of the observation fall within 3 standard deviation of mean.

Then, P (μ - 2σ < X < μ + 2σ) = 0.95

Compute the limits as follows:

`\mu-2\sigma=57-(2*8)=41\\\mu+2\sigma=57+(2*8)=73\\`

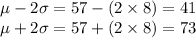
Thus, the middle 95% of completion times for all people taking the test is in the interval (41, 73).