Question

The radioisotope phosphorus-32 is used in tracers for measuring phosphorus uptake by plants. The half-life of phosphorus-32 is 14.3 days. If you begin with 30.5 mg of this isotope, what mass remains after 27.5 days have passed? Since the decomposition is a radioactive decay reaction, it is first order.

Answer 1

The mass remains after 27.5 days is 8.043 mg.

Step-by-step explanation:

Given that:

Half life = 14.3 days

`t_(1/2)=(\ln2)/(k)`

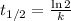
Where, k is rate constant

So,

`k=(\ln2)/(t_(1/2))`

`k=(\ln2)/(14.3)\ days^(-1)`

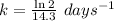
The rate constant, k = 0.04847 days⁻¹

Time = 27.5 days

Using integrated rate law for first order kinetics as:

`[A_t]=[A_0]e^(-kt)`

Where,

`[A_t]` is the concentration at time t

`[A_0]` is the initial concentration = 30.5 mg

So,

`[A_t]=30.5* e^(-0.04847* 27.5)\ mg=8.043\ mg`

The mass remains after 27.5 days is 8.043 mg.