hello!
Let's solve this inequality.
First of all, subtract 8 from both sides:-
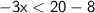
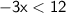
Divide both sides by -3:-

Notice that the inequality sign changed...
Here's the rule:-
When you multiply/divide both sides by a negative number, you flip the inequality sign; so if we have "less than" it becomes "greater than" and so on...
So these are the values of x that will make the inequality true:-
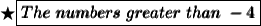
Well, -3 is greater than 4 :)
Let's plug it in and see if it makes the inequality true:-
-3>-4
Yes, it does make the inequality true :)
note:-
Hope everything is clear; if you need any clarification/explanation, kindly let me know, and I will comment and/or edit my answer :)