Question

Use the graph shown at the right.

8. What is the slope of the line?

8.

9. Find the x- and y-intercepts of the line.

9.

10. Write a direct variation equation

relating x and y.

Answer 1

Slope of the line is
`(-2)/(3)`.

x-intercept is 0 and the y-intercept is 0.

direct variation equation relating x and y is
`y=(-2)/(3)x`.

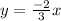Solution:

Let the points on the line are (–3, 2) and (3, –2).

`x_1=-3, y_1=2, x_2=3, y_2=-2`

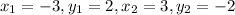
Slope of the line:

`$m=(y_2-y_1)/(x_2-x_1)`

`$m=(-2-2)/(3-(-3))`

`$m=(-4)/(3+3)`

`$m=(-4)/(6)`

`$m=(-2)/(3)`

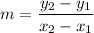
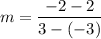
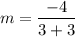
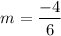
Slope of the line is
`(-2)/(3)`.

The x-intercept is, where a line crosses at x-axis.

The y-intercept is, where a line crosses at y-axis.

Here, x-intercept is 0 and the y-intercept is 0.

Direct variation form:

y = mx

`y=(-2)/(3)x`

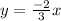
Hence slope of the line is
`(-2)/(3)`.

x-intercept is 0 and the y-intercept is 0.

direct variation equation relating x and y is
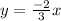`y=(-2)/(3)x`.