Answer:
(a) Mass of the water in the bucket is
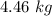 .
.
(b) The volume of water will be

Step-by-step explanation:
The question is incomplete the complete question is given below.
A farmer is using a rope and pulley to lift a bucket of water from the bottom of a well. The farmer uses a force
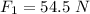 to pull the bucket of water upwards at a constant speed. The bucket, when empty, has a mass of
to pull the bucket of water upwards at a constant speed. The bucket, when empty, has a mass of
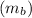 = 1.1 kg.
= 1.1 kg.
(a) Calculate the mass of the water in the bucket,
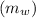 in kg
in kg
(b) Calculate the volume of the water in the bucket,
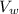 in
in
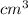 . Use density of the water 1.00 g/
. Use density of the water 1.00 g/
Given the farmer uses a force
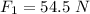 to pull out the bucket.
to pull out the bucket.
Also, the mass of the bucket
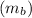 is
is
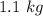
The force due to mass of bucket
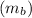 and mass of water
and mass of water
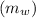 will balance the force used by farmer.
will balance the force used by farmer.
So,
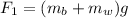

So, mass of the water in the bucket is 4.46 kg.
Now, let us work on next part.
Given density of the water
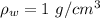

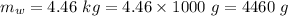
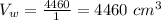
So, the volume of water will be
