Question

You are in the market for a new car. You want to check whether there is a significant difference between the fuel economy of mid-size domestic cars and mid-size import cars. You sample 22 domestic car makers and find an average fuel economy of 34.702 MPG with standard deviation of 4.718 MPG. For imports, you sample 10 cars and find an average MPG of 28.437 MPG with a standard deviation of 7.146. You use this information to calculate a 99 percentage interval for the difference in mean fuel economy of (0.435, 12.095). Of the following statements, what is the best interpretation of this interval?

1. We are 99% sure that the average difference in fuel economy of all domestic cars and all import cars is between 0.435 and 12.095.
2. We are 99% confident that the difference between the average fuel economy of all domestic mid-size cars and all import mid-size cars is between 0.435 and 12.095.
3. We are certain that the difference between the average fuel economy of all domestic mid-size cars and all import mid-size cars is between 0.435 and 12.095.
4. We do not know the population means so we do not have enough information to make an interpretation.
5. We are 99% confident that the difference between the average fuel economy of all domestic mid-size cars and all imports mid-size cars surveyed is between 0.435 and 12.095.

Answer 1

The best interpretation for this case would be:

2. We are 99% confident that the difference between the average fuel economy of all domestic mid-size cars and all import mid-size cars is between 0.435 and 12.095.

Since the confidence interval is for the population parameter not just for the surveyed info.

Step-by-step explanation:

Previous concepts

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

Solution to the problem

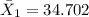`\bar X_1 = 34.702` represent the average for the fuel economy case

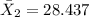`\bar X_2 = 28.437` represent the average for the import case

n1= 22 sample size for case 1

n2 = 10 sample size for case 2

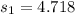`s_1 = 4.718` represent the deviation for case 1

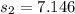`s_2 = 7.146` represent the deviation for case 2

The confidence interval for the difference of means is given by this formula:

`(x_1 -\bar x_2) \pm t_(\alpha/2) \sqrt{(s^2_(1))/(n_(1))+(s^2_(2))/(n_(2))}}`

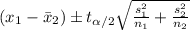
We need to find the degrees of freedom like this:

`df = n_1 +n_2 -2= 22+10-2=30`

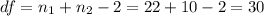
For 99% of confidence the value of the significance is
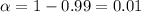`\alpha=1-0.99=0.01` and
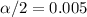`\alpha/2 =0.005` we can calculate the critical value on the t distribution with 30 degrees of freedom and we got:

`t_(\alpha/2)=2.75`

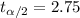
After the procedure they got for the confidence interval (0.435, 12.095)

The best interpretation for this case would be:

2. We are 99% confident that the difference between the average fuel economy of all domestic mid-size cars and all import mid-size cars is between 0.435 and 12.095.

Since the confidence interval is for the population parameter not just for the surveyed info.