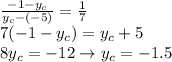1) C (9,-3.5)
2) C (17,-1.5)
Explanation:
1)
To solve this problem, we must divide the segment AB into 8 equal intervals, and then find the point sitting at 3/8 of the whole segment.
The end points of the segment in this problem are:
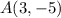
and
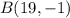
This means that the x- and y-coordinates of point C are given by the equations:
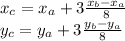
And substituting the values of the coordinates of A and B, we find:
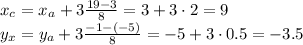
2)
In this problem, we want to find the coordinates of point C such that:
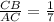 (1)
(1)
As before, the coordinates of the endpoints of the segment AB are:
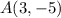
and
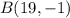
We can call the coordinates of point C as follows:

To satisfy eq.(1) for the x-coordinate, we have:

Therefore, by substitution we find:
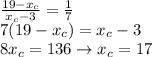
Similarly on the y-coordinate we find:
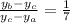
And solving we get: