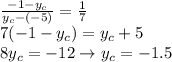Question

Given points A(3, -5) and B(19, -1), find the coordinates of point C that sit 3/8 of the way along line AB, closer to A than to B.

Given points A(3, -5) and B(19, -1), find the coordinates of point C such that CB/AC = 1/7.

Answer 1

1) C (9,-3.5)

2) C (17,-1.5)

Explanation:

1)

To solve this problem, we must divide the segment AB into 8 equal intervals, and then find the point sitting at 3/8 of the whole segment.

The end points of the segment in this problem are:

`A(3,-5)`

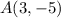
and

`B(19,-1)`

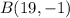
This means that the x- and y-coordinates of point C are given by the equations:

`x_c=x_a + 3(x_b-x_a)/(8)\\y_c=y_a+3(y_b-y_a)/(8)`

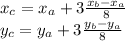
And substituting the values of the coordinates of A and B, we find:

`x_c = x_a + 3 (19-3)/(8)=3+3\cdot 2 =9\\y_x = y_a + 3 (-1-(-5))/(8)=-5+3\cdot 0.5 =-3.5`

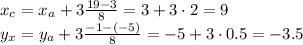
2)

In this problem, we want to find the coordinates of point C such that:

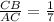`(CB)/(AC)=(1)/(7)` (1)

As before, the coordinates of the endpoints of the segment AB are:

`A(3,-5)`

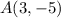
and

`B(19,-1)`

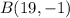
We can call the coordinates of point C as follows:

`C(x_c,y_c)`

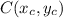
To satisfy eq.(1) for the x-coordinate, we have:

`(x_b-x_c)/(x_c-x_a)=(1)/(7)`

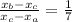
Therefore, by substitution we find:

`(19-x_c)/(x_c-3)=(1)/(7)\\7(19-x_c)=x_c-3\\8x_c=136 \rightarrow x_c = 17`

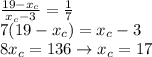
Similarly on the y-coordinate we find:

`(y_b-y_c)/(y_c-y_a)=(1)/(7)`

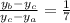
And solving we get:

`(-1-y_c)/(y_c-(-5))=(1)/(7)\\7(-1-y_c)=y_c+5\\8y_c=-12 \rightarrow y_c = -1.5`