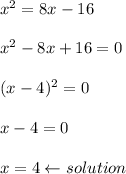Answer:
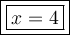
Explanation:
The equation to solve is:

1. On the left-hand side use: "The product of a constant by a logarithm is equal to the logarithm raised to the constant"
Thus, the left-hand side is:
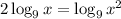
2. On the right-hand side use "The sum of two logarithms with the same base is the logarithm of the product":
Then, on the right-hand side:

3. Make them equal:
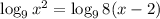
4. Since the two functions are the same, make the arguments equal:
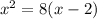
5. Solve the equation: