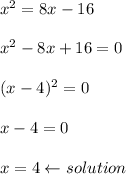Question

What is the solution to 2 log Subscript 9 Baseline (x) = log Subscript 9 Baseline 8 + log Subscript 9 Baseline (x minus 2) x = negative 4 x = negative 2 x = 4 x = 8

Answer 1

x=4

Explanation:

Answer 2

`\large\boxed{\large\boxed{x=4}}`

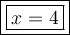
Explanation:

The equation to solve is:

`2\log_9 x=\log_9 8+\log_9 (x-2)`

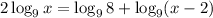
1. On the left-hand side use: "The product of a constant by a logarithm is equal to the logarithm raised to the constant"

Thus, the left-hand side is:

`2\log_9 x=\log_9 x^2`

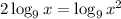
2. On the right-hand side use "The sum of two logarithms with the same base is the logarithm of the product":

Then, on the right-hand side:

`\log_9 8+\log_9 (x-2)=\log_9 8(x-2)`

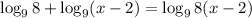
3. Make them equal:

`\log_9 x^2=\log_9 8(x-2)`

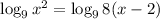
4. Since the two functions are the same, make the arguments equal:

`x^2=8(x-2)`

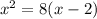
5. Solve the equation:

`x^2=8x-16\\\\x^2-8x+16=0\\\\(x-4)^2=0\\\\x-4=0\\\\x=4\leftarrow solution`