Answer:
a. $425,678.
b. 20 years
c. net present value, bond yields, spot rates, and pension obligations.
Step-by-step explanation:
a.
In order to find the present value we have to apply in the following formula
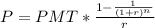
where
P = Present value of an annuity stream
PMT = Dollar amount of each annuity payment
r = Interest rate (also known as discount rate)
n = Number of periods in which payments will be made
Replacing values we have that
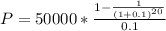
P = $425,678
b.
As written in the exercise, 20 years for a present value of $425,678
c.
The package of bonds can include net present value, bond yields, spot rates, and pension obligations.