Answer:
The equation used to solve a diode is
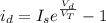
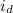 is the current going through the diode
is the current going through the diode
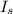 is your saturation current
is your saturation current
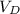 is the voltage across your diode
is the voltage across your diode
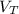 is the voltage of the diode at a certain room temperature. by default, you always use
is the voltage of the diode at a certain room temperature. by default, you always use
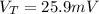 for room temperature.
for room temperature.
If you look at the equation,
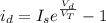 , you'd notice that the
, you'd notice that the
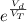 grow exponentially fast, so we can ignore the -1 in the equation because it's so small compared to the exponential.
grow exponentially fast, so we can ignore the -1 in the equation because it's so small compared to the exponential.
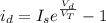
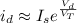
Therefore, use
 to solve your equation.
to solve your equation.
Rearrange your equation to solve for
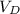 .
.

a.)
i.)
You're given
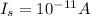
at
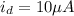 ,
,

at
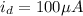 ,
,
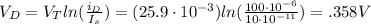
at
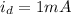 ,
,
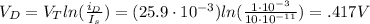
note: always use
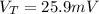
ii.)
Just repeat part (i) but change to
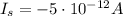
b.)
same process as part A. You do the rest of the problem by yourself.