Question

Brent is a researcher for a food company. He is on a team creating a reduced-calorie version of its flagship cracker. The team will go ahead with the development of the reduced-calorie version if the mean number of calories per serving of 6 crackers is less than 60. Brent randomly selects 26 samples of the new crackers and measures the number of calories per serving for each sample. Brent uses research conducted in the past to assume that the population is normally distributed and the population standard deviation is 0.82 calories. Use Excel to test whether the mean number of calories for each serving of the new crackers is less than 60, and then draw a conclusion in the context of the problem. Use α=0.01.

Answer 1

Explanation:

Hello!

The research team created a cracker with fewer calories. The average content of calories of the new crackers per serving of 6 should be less than 60.

To test it a random sample of 26 samples of the new cracker was taken and the calories per serving were measured.

Then the study variable is

X: calories of a 6 serve sample of the new reduced-calorie version. (cal)

The variable has a normal distribution with a population standard deviation of 0.82 cal.

To test the claim that the new crackers have on average less than 60 calories, the parameter of interest is the population mean (μ) and the hypotheses are:

H₀: μ ≥ 60

H₁: μ < 60

α: 0.01

Since the variable has a normal distribution and the population variance is known, the best statistic to use to conduct the test is a Standard Normal

`Z= ((X[bar]-Mu))/((Sigma)/(√(n)) ) ~N(0;1)`

This test is one tailed to the left, wich means that the null hypothesis will be rejected at low levels of the statistic.

`Z_(\alpha ) = Z_(0.01) = -2.334`

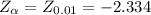
If Z ≤ -2.334, the decision is to reject the null hypothesis.

If Z > -2.334, the decision is to not reject the null hypothesis.

Using the data of the sample I've calculated the sample mean.

X[bar]= ∑X/n= 1548.61/26= 59.56 cal

`Z_(H_0)= ((59.56-60))/((0.82)/(√(26) ) ) = -2.736`

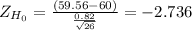
The observed Z value is less than the critical value, so the decision is to reject the null hypothesis.

At a level of significance of 1%, you can conclude that the population mean of calories of the samples of new crackers is less than 60 cal.

I hope it helps!