Question

A parallel combination of a 1.51 μ F 1.51 μF capacitor and a 2.99 μ F 2.99 μF capacitor is connected in series to a 4.41 μ F 4.41 μF capacitor. This three‑capacitor combination is connected to a 16.5 V 16.5 V battery. Find the charge of each capacitor.

Answer 1

Step-by-step explanation:

C1 = 1.51 μF

C2 = 2.99 μF

C3 = 4.41 μF

V = 16.5 V

Here C1 and C2 are connected in parallel.

Cp = C1 + C2 = 1.51 + 2.99 = 4.5 μF

C3 and Cp are in series

The equivalent capacitance is

`C=(C_(p)C_(3))/(C_(p)+C_(3))`

`C=(4.5* 4.41)/(4.5+4.41)`

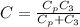
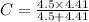
C = 2.23 μF

Let the total charge is q.

q = C x V = 2.23 x 16.5 = 36.8 μC

Voltage on C3, V3 = q / C3 = 36.8 / 4.41 = 8.35 V

Voltage on C1, V1 = Voltage on C2, V2 = V - V3 = 16.5 - 8.35 = 8.15 V

Charge on C1, q1 = C1 x V1 = 1.51 x 8.15 = 12.3 μC

Charge on C2, q2 = C2 x V2 = 2.99 x 8.15 = 24.4 μC

Charge on C3, q3 = q = 36.8 μC

Answer 2

Step-by-step explanation:

combined capacitor of parallel capacitors

1.51 + 2.99

= 4.5 μF

Resultant capacitance of all capacitor

= 4.5 x 4.41 / ( 4.5 +4.41) μF

= 2.22 μF

Charge on series capacitor

= C X V

= 16.5 X 2.22 μC

= 36.63 μC

Potential on series capacitor (4.41 μF)

= Q / C

= 36.63 / 4.41

= 8.3 V

Potential on each of parallel capacitor

= 16.5 - 8.3

= 8.2 V

Charge on 2.99 μF capacitor

= 2.99 x 8.2 = 24.52 C

Charge on 1.51 μF capacitor

= 1.51 x 8.2 =12.38 C

=