Answer:
Step-by-step explanation:
C1 = 1.51 μF
C2 = 2.99 μF
C3 = 4.41 μF
V = 16.5 V
Here C1 and C2 are connected in parallel.
Cp = C1 + C2 = 1.51 + 2.99 = 4.5 μF
C3 and Cp are in series
The equivalent capacitance is
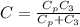
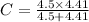
C = 2.23 μF
Let the total charge is q.
q = C x V = 2.23 x 16.5 = 36.8 μC
Voltage on C3, V3 = q / C3 = 36.8 / 4.41 = 8.35 V
Voltage on C1, V1 = Voltage on C2, V2 = V - V3 = 16.5 - 8.35 = 8.15 V
Charge on C1, q1 = C1 x V1 = 1.51 x 8.15 = 12.3 μC
Charge on C2, q2 = C2 x V2 = 2.99 x 8.15 = 24.4 μC
Charge on C3, q3 = q = 36.8 μC